1 1 2 1 3 1 N Sum Formula 10 fifa world cup south africa game 04 年 アニメ What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora For more information and source, see on this link https1 1 2 1 4 1 n sum formula A simple solution solution is to initialize sum as 0 then run a loop and call factorial function inside the loop If the function does converge toOne can write 1 1 2 1 3 ⋯ 1 n = γ ψ ( n 1) where γ is Euler's constant and ψ is the digamma function Of course, one reason for creating the

Find The Sum Of N Terms Of The Series 1 2 4 1 4 6
1+1/2+1/4+...+1/n sum formula
1+1/2+1/4+...+1/n sum formula-S=1^12^23^3n1^n1n^1 S=N^nn1^n1n2^n23^32^21^1 Sum formula=2n=(1an)(4an1)(an1) First term= last term A1=an Medium same for upper and lower =an1 A3=an2 If 1^12^23^34^4100^100 3 Add a comment 6 According to Wikipedia S = n * (n 1) * (2*n 1) / 6 It is easy to prove this using induction Share edited Aug 1 '12 at 1745




A Using Formula 2 Find The Sum Of The Series Chegg Com
To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=1234 1 (1/2) (1/3) – (1/4) = Recommended Please try your approach on {IDE} first, before moving on to the solution Approach The idea is to form a recursive case and base case in order to solve this problem using recursion For your first sequence a_1=(1)^(11)(14)=5 a_2=(1)^(21)(24)=6 continue for each term Replace n by the whole number indicating the term you are calculating A sequence is a list of terms in a specific order, the order is given by n, the value is given when you substitute n into the formula
This is an arithmetic series, and the equation for the total number of times is (n 1)*n / 2 Example if the size of the list is N = 5, then you do 4 3 2 1 = 10 swaps and notice that 10 is the same as 4 * 5 / 2To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(11/2)(11/3)(11/4)(11/(n1))` Ex 41, 4 Prove the following by using the principle of mathematical induction for all n ∈ N 123 234 n(n 1) (n 2) = (𝑛(𝑛 1)(𝑛 2)(
S = 1 1/2 1/4 1/8 so, if we multiply it by 1/2, we get (1/2) S = 1/2 1/4 1/8 1/16 Now, if we subtract the second equation from the first, the 1/2, 1/4, 1/8, etc all cancel, and we get S (1/2)S = 1 which means S/2 = 1 and so S = 2The infinite series whose terms are the natural numbers 1 2 3 4 ⋯ is a divergent series The nth partial sum of the series is the triangular number ∑ k = 1 n k = n 2, {\displaystyle \sum _{k=1}^{n}k={\frac {n}{2}},} which increases without bound as n goes to infinity Because the sequence of partial sums fails to converge to a finite limit, the series does not have a sumCalculus Tests of Convergence / Divergence Partial Sums of Infinite Series 1 Answer Steve M I won't go into a full explanation as it too complex But essentially
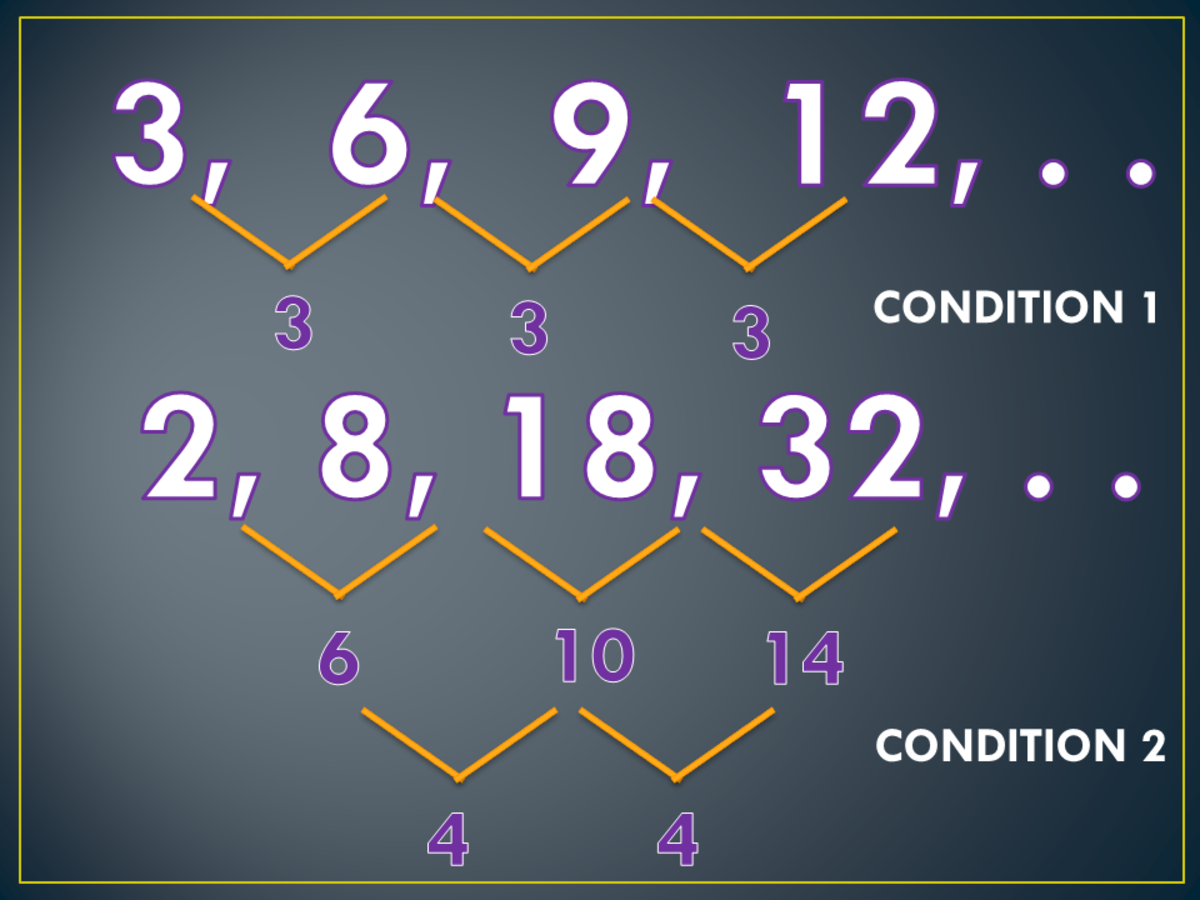



How To Find The General Term Of Sequences Owlcation




Geometric Series Wikipedia
Establish A Formula For The Product 1 1 2 1 1 3 1 1 N Stumbling Robot Save Image Proof Of 1 2 2 2 Cdots N 2 N 3 3 N 2 2 N 6 Mathematics Stack Exchange Save Image Solved Prove That 1 N 1 1 N 2 1 2n 1 1 Chegg Com Save Image Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot Save Image 1234n Formula Save Image Squared TriangularHow long after firing does it reach the maximum height?N4 1 2 n3 1 4 n2 Finding this formula was the hard part It is now not so hard to prove this formula by induction Proof We will prove that (8) 1 3 2 1 n3 = 4 n4 1 2 n3 1 4 n2 by induction on n The case n= 0 is clear, because both sides of the equation are equal to 0 If (8) is true for n= m 1, then




Prove That 1 3 2 3 3 3 N 3 N N 1 2 2 Teachoo



Establish A Formula For The Product 1 1 2 1 1 3 1 1 N Stumbling Robot
94 Little ant said 1^2 2^2 3^2 2^n = 2^ (n1) This makes absolutely no sense I mean, look at it for a second firstly you failed to notice the pattern correctly since 2^n means 2^12^22^3 instead of what is shown And secondly, how can that all equal 2^ (n1) when on the left side of the equation, you already have 2^n which means What is the sum of the series 1/1, 1/2, 1/3, 1/n and 1/1, 1/4, 1/91/n^2 where n is finite?SOLUTION Let f (n) = 1/2 1/3 1/4 1/5 1/6 1/7 1/n Find a recursive formula for f (n) Do not forget to include any necessary base case (s) SOLUTION Let f (n) = 1/2 1/3 1/4 1/5 1/6 1/7 1/n Find a recursive formula for f (n) Do not forget to




Basel Problem Wikipedia




5 4 Mathematical Induction T
Use the distributive property to multiply a n by 2 n − 1 Use the distributive property to multiply 2a_ {n}na_ {n} by 2n1 and combine like terms Use the distributive property to multiply 2 a n n − a n by 2 n 1 and combine like terms Subtract 4n^ {2} from both sides Subtract 4 n 2 from both sidesClick here👆to get an answer to your question ️ Solve the equation 4 ( 1 ) 2 ···x = 437To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `1/121/231/341/(n(n1))=n/(n1),n in N` is true for




n Sum Formula



1
Simple and best practice solution for (1)/(2)n1=4 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itEstablish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot For more information and source, see on this link http//wwwstumblingrobotcom//establishaformulafor Transcript Prove 1 2 3 n = (n(n1))/2 for n, n is a natural number Step 1 Let P(n) (the given statement)\ Let P(n) 1 2 3 n = (n(n1))/2 Step




Harmonic Series Mathematics Wikipedia




Sum Of N N Or N Brilliant Math Science Wiki
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyThe partial sums form a convergent sequence 1, 2/3, 1, 4/5, 1, 6/7, The sequence converges to 1 Grouping pairs of successive terms leads to every other sum being omitted but does not change the fact of convergence, nor affects the limit itself The second series to consider is 1/1 2/3 2/3 3/5 3/5 4/71/24 1/2=n what is the solution a tower the tower is 6096 ft high the height of the object above the ground seconds after firing is given by the formula h () = 16 ² 80 0 what is the maximum height reached by the object?



1



Sum Of The Series 1 2 1 2 1 3 1 4 1 2 2 1 3 2 1 6 1 2 3 1 3 3 Oo Youtube
Find a formula for (11/2) (11/3?)(1 1/4?)(11/n?) for n>=2, and use the principle of mathematical induction to prove that the formula is correct QuestionAn=2* (1/4)n Simple and best practice solution for an=2* (1/4)n equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkSOLUTION 1/21/41/81/2^n=11/2^n prove by mathematical induction that above statement holds true for every integer n belongs to N HINTto prove that 11/2^ (k1) Algebra Sequences of numbers, series and how to sum them Section Solvers Solvers Lessons Lessons




n2 Formula Proof



Finding The Sum Of Consecutive Numbers
It's called nth Harmonic Number and yes, there is a formulaFind an answer to your question write formula for 1234n lakhwinderkourg lakhwinderkourg Math Secondary School answered Write formula for 1234n 2 See answersTwo sample induction problems 1 Find a formula for 1 4 7 (3n 2) for positive integers n, and then verify your formula by mathematical induction



Solved N N 2 1 N 2 4 3n 1 3n 6 Solve The Equation Record The Answers As Exact Values Course Hero




What Is The Solution To The Equation 1 Over 2 N 8 N 4 N 6
21 For the proof, we will count the number of dots in T (n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreWrite formula for 1234n lakhwinderkourg is waiting for your help Add your answer and earn points



Question Corner Tetrahedral And 4 Tetrahedral Numbers




Proof 1 1 1 4 1 9 1 16 1 25 Pi 2 6 Youtube
Program to find sum of series 1 1/2 1/3 1/4 1/n If inverse of , 1/ (a d), 1/ (a 2d), 1/ (a 3d) 1/ (a nd) where "a" is the 1st term of Program to Find out Distance Travelled by the Equation d = ut at^2 in C Programming asked in GTU BE (CSEISem) Programming For Problem Solving Lab by Aditya Chodhary Goeduhub's Expert ( 71k points)Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot For more information and source, see on this link http//wwwstumblingrobotcom//establishaformulaforn2/ Solved Prove That 1 N 1 1 N 2 1 2n 1 1 Chegg Com




Formula 1 2 3 4




What Is The Sum Of 1 1 3 2 1 3 3 1 3 N Quora
Originally Answered Is there a formula for calculating 1 1/2 1/3 1/4 1/n for any whole number n? The binomial series is the Maclaurin series for f (x)= (1x)^r It converges for x Tracing Numbers 1 2 3 4 5 Worksheet Preschool Number Worksheets Numbers Preschool Tracing Worksheets Preschool



What Is The Sum Of 1 2 1 4 1 8 Mathematics And Calculus




4 Ways To Find Any Term Of An Arithmetic Sequence Wikihow
Sum of n, n², or n³ n n are positive integers Each of these series can be calculated through a closedform formula The case 5050 5050 5050 ∑ k = 1 n k = n ( n 1) 2 ∑ k = 1 n k 2 = n ( n 1) ( 2 n 1) 6 ∑ k = 1 n k 3 = n 2 ( n 1) 2 4The first thing we notice is that for n > 1, we are just adding another fraction to the previous value of f (n) So we can construct f (n) = f (n1) 1/ (n (n1)) Now look at the small values of n f (1) = 1/2, f (2) = 1/2 1/6 = 2/3, f (3) = 2/3 1/12 = 3/4, f (4) = 3/4 1/ = 4/5, etc Enter the world of Formula 1 Your goto source for the latest F1 news, video highlights, GP results, live timing, indepth analysis and expert commentary




Show That The Sum Of The Cubes Of The First N Natural Numbers Equal




Program For Factorial Of A Number Geeksforgeeks
34 Noninductive derivation ∑ k = 1 n ( 3 k − 2) = ∑ k = 1 n 3 k − ∑ k = 1 n 2 = 3 ( ∑ k = 1 n k) − 2 n = 3 ( n) ( n 1) 2 − 4 n 2 = 3 n 2 − n 2 = n ( 3 n − 1) 2 This, of course, relies on one knowing the sum of the first n natural numbers, but that's a1 1 • n 1 = — = ————— 1 n Equivalent fraction The fraction thus generated looks different but has the same value as the whole Common denominator The equivalent fraction and the other fraction involved in the calculation share the same denominatorCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Paradox 1 1 2 1 3 1 4 0 The Simpsons And Their Mathematical Secrets



Reactions Of Dienes 1 2 And 1 4 Addition Master Organic Chemistry
31 Adding a whole to a fraction Rewrite the whole as a fraction using 4 as the denominator (n 1) 3 (n 1) 3 • 4 (n 1) 3 = ———————— = ———————————— 1 4 Equivalent fraction The fraction thus generated looks different but has the same value as the wholeNot prime The LCM of 1, 1, 1 1, 1, 1 is the result of multiplying all prime factors the greatest number of times they occur in either number 1 1 The factor for n − 1 n 1 is n − 1 n 1 itself ( n − 1) = n − 1 ( n 1) = n 1 ( n − 1) ( n 1) occurs 1 1 time The factor for n 1 n 1 is n 1 n 1 itself




Pdf Kind Of Proofs Of Ramanujan Like Series



Recursive Formula Of A Sequence




1 2 1 4 1 8 1 16 Wikipedia
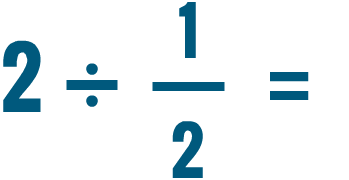



Fractions Multiplying And Dividing Fractions




What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora



1 2 3 4 Wikipedia




Answered In Exercises 1 4 Use The Principle Of Bartleby




Finite Geometric Series Formula Video Khan Academy



Http Www Math Pitt Edu Athanas Math 0230 Calculus Ii Practice8answers Pdf




Find The Sum Of The Series 1 2 4 Upto 9 Terms Using The Formula



1




Arithmetic Sequences And Series 1
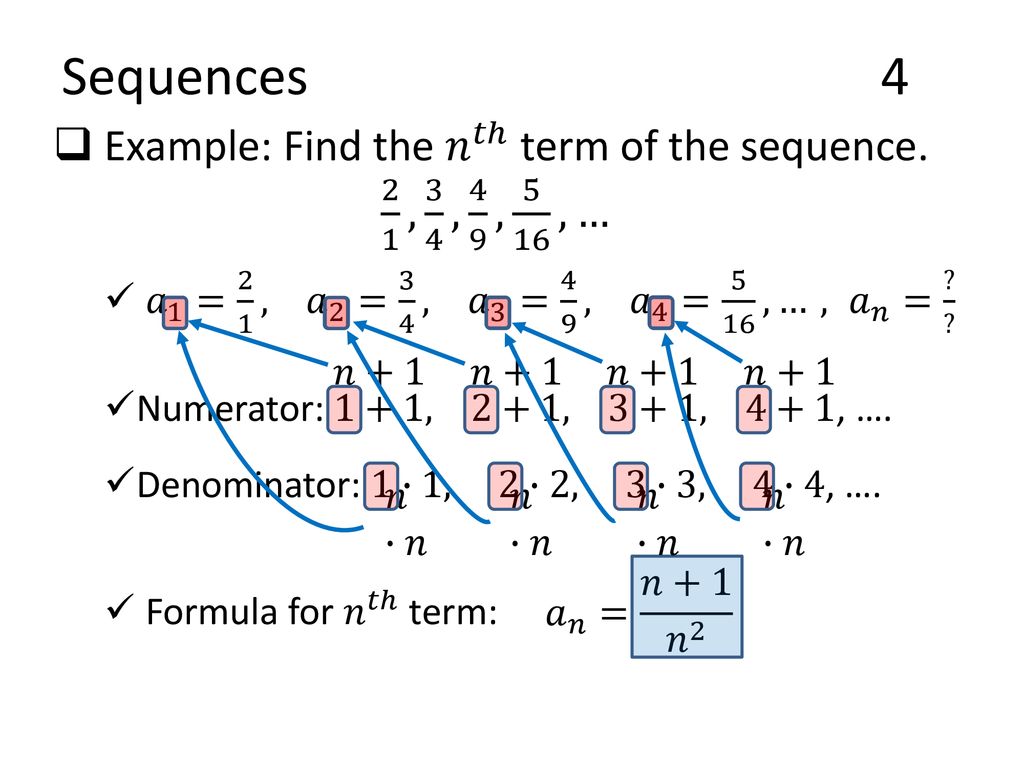



Sequences The Binomial Theorem Chapter Ppt Download



What Is The Name For The Pattern 1 2 4 8 16 What Is The Formula To Determine A Known Position In The Pattern Quora



1
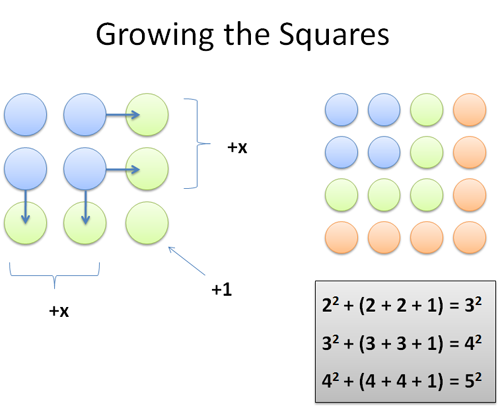



Surprising Patterns In The Square Numbers 1 4 9 16 Betterexplained
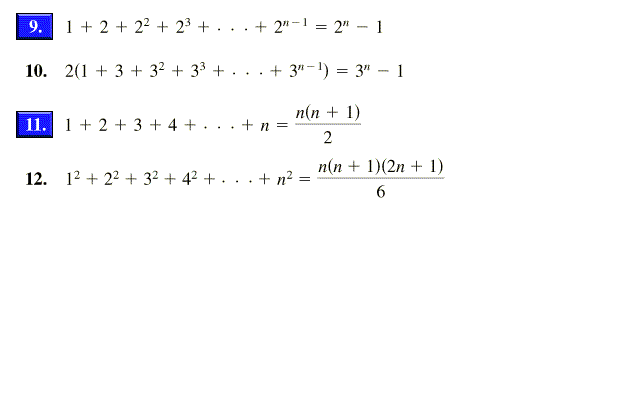



In Exercises 5 18 Use Mathematical Induction To Chegg Com




Discrete Mathematics Online Presentation




Permutations By Inversion
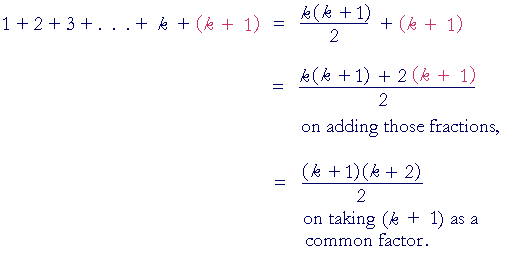



Mathematical Induction Topics In Precalculus
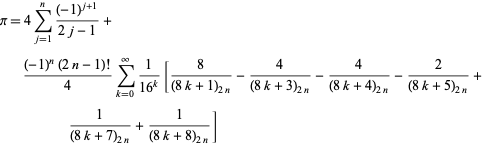



Pi Formulas From Wolfram Mathworld




Prove That 1 N 1 1 N 2 1 2n 1 1 2 Chegg Com




Ex 4 1 11 Prove 1 1 2 3 1 2 3 4 1 3 4 5 1 N N 1 N 2



Http Www Math Niu Edu Jthunder Courses 08spring 230 Sec2 Quiz7ans Pdf




How To Explain And Element Of The 1 2 1 4 Series Proof Mathematics Stack Exchange
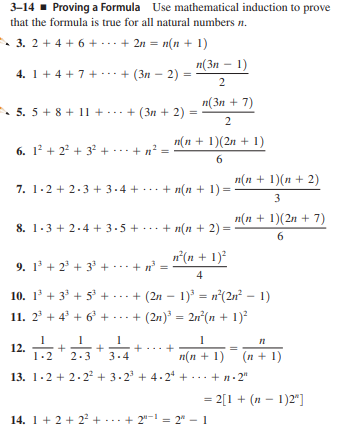



Answered 3 14 Proving A Formula Use Bartleby




Prove Using Pmi 1 1 4 1 9 1 16 1 N 2 2 1 N For All N 2 N Maths Principle Of Mathematical Induction Meritnation Com



Http Www Jsums Edu Nmeghanathan Files 16 01 Csc323 Sp16 Qb Module 1 Efficiency Of Algorithms Pdf X
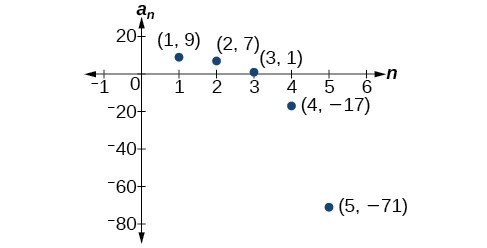



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




Give The Definition In Formula Of The Sequence 2 1 Chegg Com




Find The Sum Of N Terms Of The Series 1 2 4 1 4 6




Using Arithmetic Sequences Formulas Algebra Video Khan Academy




1234n Formula



Python Challenges 1 Exercises Practice Solution W3resource




A Using Formula 2 Find The Sum Of The Series Chegg Com




Proof Of 1 2 2 2 Cdots N 2 N 3 3 N 2 2 N 6 Mathematics Stack Exchange




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 19 Arithmetic Progressions Download Free Pdf




In Exercises 5 18 Use Mathematical Induction To Chegg Com




Sum Of N N Or N Brilliant Math Science Wiki




Sequences The Binomial Theorem Chapter Ppt Download




What Is 6 2 1 2 The Correct Answer Explained Mind Your Decisions




How To 12 Proof By Induction 1 3 2 3 3 3 N 3 N N 1 2 2 N 2 N 1 2 4 Prove Mathgotserved Youtube




Ex 4 1 9 Prove 1 2 1 4 1 8 1 2n 1 1 2n



How Does 1 2 1 4 1 8 1 16 Till Infinity Have A Sum Quora



Example Of 2d Convolution




Infinite Series



Faculty Math Illinois Edu Hildebr 213 Inductionsampler Pdf




A Sequence Is Shown Below 1 4 1 2 Select The Gauthmath




Ali Added The Following Series If Fraction How Many More Fraction In This Series He Must Add To Get The Answer Equal To Onevor More Than One 1 2 1 4 1 Mathematics Topperlearning Com 8ycaaeuu




Ex 4 1 9 Prove 1 2 1 4 1 8 1 2n 1 1 2n
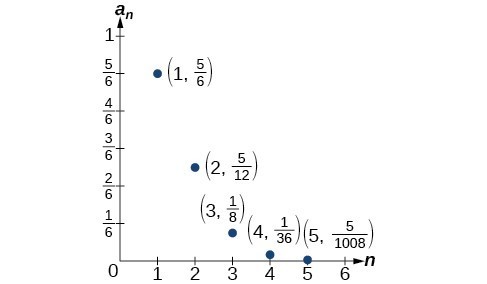



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




Sequences Arithmetic Sequences Examples




Geometric Series Wikipedia
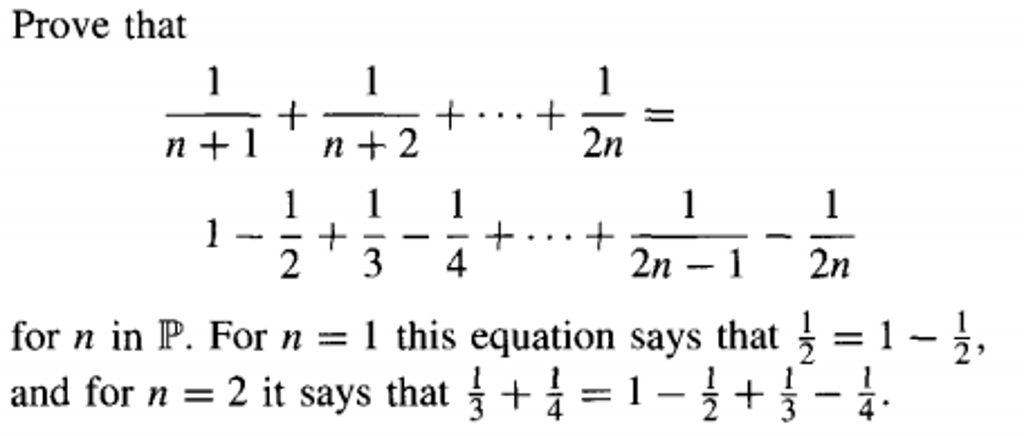



Prove That 1 N 1 1 N 2 1 2n 1 1 2 Chegg Com



Faculty Math Illinois Edu Jpascale Courses 11 M408d Notes Hw4 Sol Pdf




Solving Rational Equations
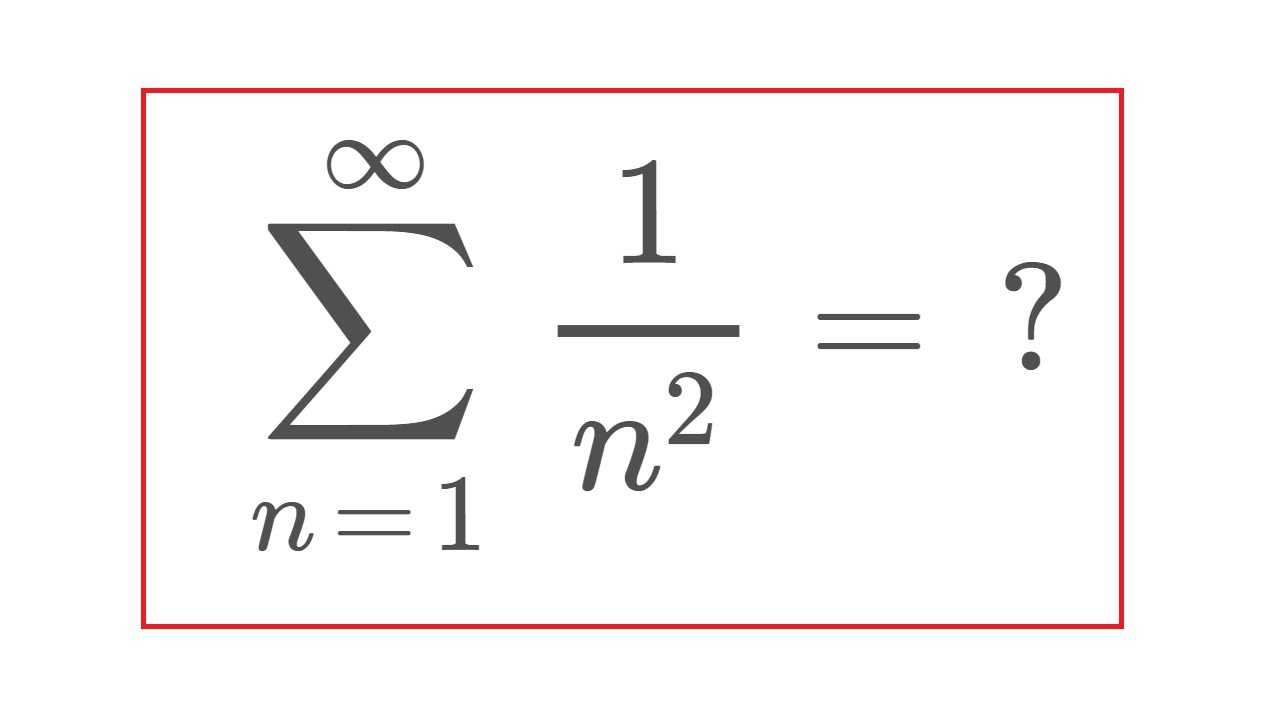



Sum Of 1 N 2 Youtube




n2 Formula



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot




1 2 1 4 1 8 1 16 Wikipedia




Show That Infinity Pi N 1 1 4 2n 1 2 Chegg Com




Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange




How To Proceed Further In This Arithmetico Geometric Progression Problem Mathematics Stack Exchange




Arithmetic Sequence Formula Chilimath




How To Derive N 1 2 From 1 2 3 N N Quora



Verify A Summation Formula For Sin3 X Stumbling Robot




How To Find The General Term Of Sequences Owlcation




Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy




Consider The Conditionally Convergent Series Chegg Com




The Catalan Numbers And Their Applications 1 2




A Use Gauss S Approach To Find The Following Sum Math 2 4 6 Ldots 100 Math B Use Gauss S Approach To Find A Formula For The Sum Of



What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora



What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora
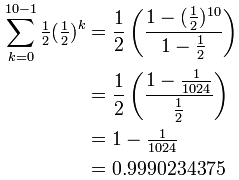



Geometric Sequences And Sums




How To Solve Fraction Questions In Math 10 Steps With Pictures



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot




Find The Sum Of The Following Series 1 2 1 3 2 1 2 3 1 3 4



Infinite Series



0 件のコメント:
コメントを投稿